Estratégias para Solução de Problemas de Otimização Combinatória

Fernando Mario de Oliveira Filho
Orientador: Carlos Eduardo Ferreira
Supervisora: Yoshiko Wakabayashi

Abstract:

Neste trabalho abordamos o problema de Steiner com grupos, que consiste em dado um grafo com custos nas arestas e uma coleção de subconjuntos do conjunto de vértices, encontrar um subgrafo que conecte pelo menos um vértice de cada conjunto da coleção e que tenha custo mínimo. O problema é uma generalização do problema de Steiner em grafos e surge naturalmente no desenvolvimento de circuitos VLSI. Apresentamos estudos feitos para o desenvolvimento de um algoritmo seguindo a estratégia branch-and-cut para o problema. O trabalho se baseia num projeto de iniciação científica que teve apoio da FAPESP e que foi desenvolvido desde Agosto de 2001 até Agosto de 2003.


Contents

Introdução

Problemas de otimização combinatória podem ser definidos, de forma geral, da seguinte maneira: dado um conjunto finito $S$ e uma função custo definida sobre este conjunto, encontrar um elemento de $S$ que maximiza/minimiza esta função. Um exemplo de problema de otimização combinatória é o problema da árvore geradora mínima, em que nos é dado um grafo conexo $G$ com custos nas arestas e pede-se uma árvore geradora de $G$ que tenha custo mínimo.

O problema da árvore geradora mínima, assim como muitos outros problemas de otimização combinatória, pode ser resolvido por algoritmos eficientes (algoritmos que gastam tempo polinomial no tamanho da entrada). Para muitos outros problemas, entretanto, não conhecemos algoritmos eficientes (e provavelmente eles não existem). Muitos destes problemas ``difíceis'' têm importantes aplicações práticas, como é o caso do problema de Steiner com grupos. Este problema consiste em, dado um grafo com custos nas arestas e uma coleção de conjuntos de vértices deste grafo, encontrar um subgrafo de custo mínimo que conecte pelo menos um vértice de cada conjunto dado. Este problema é uma generalização do problema de Steiner em grafos (que corresponde ao caso em que cada conjunto dado é unitário) e é útil para o desenvolvimento de circuitos VLSI.

Durante o projeto estudamos problemas clássicos de otimização combinatória e, no último ano, concentramos os estudos no problema de Steiner com grupos. Estudamos algumas formulações para o problema de Steiner com grupos com vistas a obtenção de limitantes inferiores, que seriam então utilizados num algoritmo branch-and-cut para o problema. Estudamos também algoritmos de aproximação para o problema, que podem ser utilizados na obtenção de soluções viáveis. Estudamos também outro aspecto importante para o desenvolvimento de um algoritmo exato para o problema, os testes de redução. Tais testes nos permitem reduzir o tamanho do grafo de entrada consideravelmente antes de começar o processo de branching, o que permite atacar instâncias muito maiores. Estes estudos culminaram no desenvolvimento de um algoritmo exato para o problema de Steiner com grupos seguindo a estratégia branch-and-cut.


Circuitos VLSI e o Problema de Steiner com Grupos

A maioria dos processadores usados atualmente são fabricados com a tecnologia de circuitos integrados VLSI (very-large-scale integration). A confecção de um circuito VLSI é composta de várias fases, dentre as quais duas são de especial importância: a fase de colocação (placement) e a de roteamento (routing). A fase de colocação precede a fase de roteamento. Durante a fase de colocação os vários componentes são dipostos na placa de circuito. Estes componentes variam de simples portas lógicas até complexos circuitos. Após a fase de colocação temos a fase de roteamento, durante a qual nosso objetivo é conectar os diversos componentes através de redes condutoras. 1

O modelo apropriado para o problema do roteamento é o modelo da rede retilinear. Uma rede retilinear é um grafo cujos vértices são identificados com pontos no plano e cujas arestas são identificadas com segmentos verticais ou horizontais que ligam pontos no plano. A cada aresta também temos um custo associado, que pode ser o comprimento do segmento que ela representa ou outra grandeza apropriada. Observe que, mesmo que as arestas tenham custo igual a seu comprimento, a distância entre dois vértices do grafo não necessariamente é igual à distância retilinear2 entre os dois pontos no plano: podemos ter ``buracos'' no grafo, representando regiões do circuito não disponíveis para o roteamento. A Figura 1 apresenta um exemplo de uma rede retilinear.


\begin{myfigure}{htbp} \includegraphics{problema.1} \legenda{Uma rede retilinear... ...ede que conecta os componentes esta destacada em linhas grossas.} \end{myfigure}

Dada uma rede retilinear representando um circuito, sabemos quais são os vértices que queremos ligar através da rede condutora. Nosso problema é então o de determinar qual a rede condutora de menor custo que conecta todos os componentes entre si. No caso em que as arestas tem custo igual ao comprimento dos segmentos que representam, queremos encontrar uma rede de menor comprimento possível. O problema de Steiner em grafos é uma generalização do problema que acabamos de descrever para redes retilineares. Dados um grafo $G$ e um conjunto não-vazio $Z \subseteq V_G$, dizemos que um conjunto $S \subseteq E_G$ é $Z$-gerador se $G[S]$ contém pelo menos um caminho entre cada par de vértices $r, s \in Z$. Com isso podemos definir formalmente o problema de Steiner em grafos.


\begin{problema}{\textsc{PSG}\,$(G, Z, c)$} Dados um grafo $G$, um conjunto $Z \... ...zido por um conjunto $Z$-gerador e que minimize $c(T) := c(E_T)$. \end{problema}

Chamamos os vértices do conjunto $Z$ de terminais e os demais vértices de $G$ de não-terminais ou vértices de Steiner. É fácil ver como usar este problema para resolver o problema do roteamento descrito anteriormente. Basta considerar o conjunto $Z$ de terminais como sendo o conjunto dos vértices correspondentes aos conectores de cada componente do circuito.

O PSG já foi amplamente estudado [Fer89,HRW92] e é bastante utilizado para modelar problemas de roteamento. Ele não leva em consideração, entretanto, um fator adicional que poderia nos permitir obter soluções mais baratas para o problema do roteamento. Observe pela Figura 1 que cada componente pode ser rotacionado ou espelhado após sua localização na placa ter sido determinada. Através de rotações e espelhamentos, a posição do pino conector de um componente pode variar, conforme ilustra a Figura 2. Para cada possível localização dos pinos conectores dos componentes temos uma solução ótima diferente para o PSG. É razoável querer obter a melhor dentre todas tais soluções.


\begin{myfigure}{htbp} \includegraphics{problema.2} \legenda{Os quatro possíveis... ...nente e a posição final do pino conector após cada espelhamento.} \end{myfigure}

Foi neste contexto que Reich e Widmayer [RW90] introduziram o problema de Steiner com grupos. Para definirmos este problema, considere um grafo $G$ e uma coleção $\Rcal$ de subconjuntos de $V_G$. Dizemos que um conjunto $S \subseteq E_G$ é $\Rcal$-gerador se $G[S]$ contém um componente conexo com pelo menos um vértice de cada conjunto de $\Rcal$. Com isso, o problema de Steiner com grupos é o seguinte:


\begin{problema}{\textsc{PSGrp}\,$(G, \Rcal, c)$} Dados um grafo $G$, uma coleçã... ... por um conjunto $\Rcal$-gerador e que minimize $c(T) := c(E_T)$. \end{problema}

Chamamos os conjuntos de $\Rcal$ de grupos. Se $v \in V_G$ pertence a algum grupo então $v$ é um vértice de grupo. Caso contrário, $v$ é um não-terminal ou vértice de Steiner. Denotamos por $\Rch$ o conjunto de todos os vértices de grupo. Podemos modelar o problema de roteamento da Figura 1 utilizando o problema de Steiner com grupos, bastando considerar para cada componente um grupo contendo os possíveis conectores daquele componente, levando-se em conta todas as rotações e espelhamentos possíveis. A Figura 3 mostra o resultado obtido. Observe que conseguimos um roteamento de custo menor que o obtido pela aplicação do PSG.


\begin{myfigure} % latex2html id marker 203 {htbp} \includegraphics{problema.3} ... ...e roteamento do circuito da Figura~\ref{fig:roteamento_steiner}.} \end{myfigure}

Sabemos que o PSG é NP-difícil [Kar72]. O PSGRP, por ser uma generalização do PSG, também é NP-difícil. Na verdade, existem resultados mais fortes acerca da complexidade de aproximar o PSGRP [GKR00].

Um Algoritmo Branch-and-Cut

Introdução

No método branch-and-cut nós dividimos o problema em subproblemas, resolvendo-os de modo a encontrar a solução ótima. Para tanto, consideramos subproblemas que incluem ou excluem uma determinada aresta.

Por exemplo, podemos considerar o subproblema do problema original que inclui a aresta $e$ ou que exclui esta aresta. Podemos dividir os subproblemas em outros subproblemas, fixando mais arestas, até obter problemas que podemos resolver. Podemos representar isto por uma árvore de decisão, como ilustra a Figura 4.


\begin{myfigure}{htbp} \begin{center} \includegraphics{problema.7} \end{center}\... ... $S_{ef}^{10}$\ podem ser eliminados com base nestes limitantes.} \end{myfigure}

Entretanto, se fixarmos todas as variáveis de todas as formas possíveis teremos um algoritmo extremamente ineficiente. Uma idéia é então calcular para cada nó da árvore (ou seja, para cada subproblema) um limitante inferior e um limitante superior para o valor da solução ótima daquele subproblema. Assim, podemos determinar quais nós são infrutíferos, tornando a busca pelo ótimo mais eficiente. A Figura 4 ilustra situações em que podemos eliminar nós da árvore de decisão.

Testes de redução

Antes de iniciar o método branch-and-cut, é útil tentar diminuir o máximo possível o tamanho do grafo de entrada. Para tanto, utilizamos testes de redução, que tentam identificar arestas ou vértices que não ocorrem em pelo menos uma solução ótima e removê-los. Testes de redução para o PSG foram estudados por diversos autores, destacamos os trabalhos [DV89,Dui94,UAR99,RZ00]. Muitos destes testes podem ser facilmente adaptados ao PSGRP.

Como um exemplo, considere o seguinte teorema:


\begin{teorema}{} Seja $(G, \Rcal, c)$\ uma instância do \textsc{PSGrp}\ e $e = ... ...corre em nenhuma solução ótima do $\textsc{PSGrp}\,(G, \Rcal, c)$. \end{teorema}


\begin{prova}{} Seja $T$\ uma solução ótima do $\textsc{PSGrp}\,(G, \Rcal, c)$\ ... ... para o \textsc{PSGrp}\ de custo inferior a $c(T)$, uma contradição. \end{prova}

Este é apenas um exemplo de teste de redução. Muitos outros testes mais complexos e elaborados permitem reduções significativas no tamanho do grafo de entrada.

Outros tipos de redução podem ser aplicados durante a solução do problema. Este é o caso da fixação por custo reduzido, que nos permite fixar variáveis do problema com base na base ótima encontrada durante a solução do problema de programação linear que utilizamos para calcular limitantes inferiores para o valor do ótimo.

Limitantes inferiores

Para encontrar limitantes inferiores na estratégia branch-and-cut utilizamos uma relaxação linear do problema em questão e dados sobre poliedros associados ao problema para fortalecer esta relaxação. Para descrevermos a relaxação usada para o PSGRP vamos introduzir uma nova definição. Dada uma instância $(G, \Rcal, c)$ do PSGRP, um conjunto $S \subseteq V_G$ é chamado de $\Rcal$-separador se existem grupos $R_1, R_2 \in \Rcal$ tais que $R_1 \subseteq S$ e $R_2 \cap S = \emptyset$. Um corte $\delta(S)$ é $\Rcal$-separador se $S$ for $\Rcal$-separador. Obviamente, toda solução ótima do PSGRP contém pelo menos uma aresta de cada corte $\Rcal$-separador.

Com isso, podemos considerar a formulação em que associamos a cada aresta $e$ uma variável $x_e$ que é $1$ se a aresta está na solução ou $0$ caso contrário. Encontrar uma solução ótima do $\textsc{PSGrp}\,(G, \Rcal, c)$ é então o mesmo que resolver o problema de programação inteira
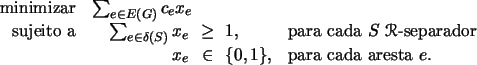
\begin{linearprogram} \mbox{minimizar}& \lalig{\sum_{e \in E(G)} c_e x_e}&&&\\ ... ... \par & x_e & \in & \{ 0, 1 \},&\mbox{para cada aresta $e$.} \end{linearprogram}

Claramente, resolver o problema acima é tão difícil quanto resolver o problema original. Sua relaxação linear, entretanto, pode ser resolvida em tempo polinomial, graças ao fato de sabermos separar em tempo polinomial as inequações de corte. Assim, podemos resolver em tempo polinomial o problema
\begin{linearprogram} \mbox{minimizar}& \lalig{\sum_{e \in E(G)} c_e x_e}&&&\\ ... ...r}\\ \par & x_e & \in & [0, 1],&\mbox{para cada aresta $e$} \end{linearprogram}

e sua solução ótima nos fornece um limitante inferior para a solução ótima do problema original. Usamos este limitante em nosso algoritmo.

Limitantes superiores

Limitantes superiores podem ser obtidos utilizando-se heurísticas que encontram soluções viáveis para o problema. Em nosso algoritmo, utilizamos heurísticas baseadas na solução da relaxação linear descrita na seção anterior.

A solução ótima $x^*$ da relaxação linear discutida tem uma interessante propriedade capaz de nos ajudar no desenvolvimento de heurísticas capazes de encontrar soluções viáveis para o PSGRP:


\begin{proposicao}{} Se $x^*$\ é uma solução ótima da relaxação linear apresenta... ...o e contém um vértice de cada grupo de $\Rcal$.\hfill\qedsymbol \end{proposicao}

No programa, permitimos apenas custos positivos. Com isso, a heurística que utilizamos encontra o grafo suporte da solução da relaxação linear e nele encontra uma árvore geradora mínima. Esta árvore é uma solução do PSGRP. Testamos também algumas outras heurísticas simples, mas esta se mostrou mais eficaz que as demais.

Nossos objetivos e o que foi feito

O objetivo original do projeto de iniciação científica, que teve início em Agosto de 2001, era num primeiro momento estudar problemas clássicos de otimização combinatória e o método dos planos-de-corte e num segundo momento estudar um problema difícil de otimização combinatória e os resultados conhecidos sobre ele.

No primeiro período da iniciação estudamos diversos problemas clássicos de otimização combinatória, como o problema da árvore geradora mínima ou o problema do fluxo máximo. No segundo período, escolhemos o problema de Steiner com grupos como objeto de estudo. Estudamos algoritmos de aproximação que foram propostos para o problema e também alguns poliedros associados a ele, assim como testes de redução. O próximo passo foi o desenvolvimento de um algoritmo exato para o problema, utilizando a estratégia branch-and-cut.

O BCC e a Iniciação Científica

Nesta seção tentarei explorar um pouco da relação entre o BCC e o meu projeto de iniciação científica.

As disciplinas

Considero que cada disciplina oferecida tenha pelo menos algum papel na formação do aluno, exceto disciplinas de utilidade obviamente duvidosa, como Física I e II. As disciplinas de matemática, por exemplo, foram de extrema importância por exigirem um tipo de raciocínio com o qual o aluno não está acostumado quando entra no curso, sendo este um pré-requisito de muitas outras disciplinas de computação.

Entre as disciplinas de computação, excluindo as disciplinas básicas (que são obviamente importantes), as que mais me ajudaram em meu projeto foram:

As disciplinas que envolvem programação de grandes projetos, como Laboratório de Programação e Sistemas Operacionais, também foram de grande ajuda por fornecer a prática necessária ao desenvolvimento de um programa complexo como o que foi feito.

Todas as demais disciplinas me ajudaram pelo menos a conhecer algumas outras áreas da computação.

Desafios e frustrações

A área de otimização combinatória, pela qual me interessei desde o segundo ano, é extremamente desafiadora. Ela é provavelmente a área de ciência da computação que mais cresceu nos últimos anos e continua crescendo rapidamente.

Considero que o mais interessante nesta área seja a forte relação com a matemática. Muitos dos problemas abertos mais intrigantes da computação e matemática atuais são problemas de otimização combinatória.

Dito isto, obviamente houve muitas frustrações. Muitos dos resultados existentes para o PSGRP, por exemplo, parecem fracos a primera vista e podemos ser levados a acreditar que resultados mais fortes podem ser obtidos facilmente. Este certamente não é o caso.

Conclusão

O projeto de Iniciação Científica serviu não só de base para o projeto de Mestrado que desenvolverei no próximo ano como também me ajudou a conhecer mais sobre diversas áreas da Ciência da Computação e as relações entre elas.

A estrutura do curso foi fundamental para o desenvovimento do projeto, oferencendo uma forte base para que estudos mais profundos em diversas áreas possam ser efetuados pelo aluno. A experiência obtida em diversas das disciplinas foi fundamental para o desenvolvimento do projeto.

Outro aspecto que considero importante foi a interação com o orientador, que me levou a conhecer mais sobre a dinâmica de uma pesquisa. A interação com muitos outros professores, que ajudaram direta ou indiretamente no projeto, também foi muito proveitosa e interessante.

Isto ressalta um aspecto importante do curso: a diversidade dos tópicos cobertos. Aliadas às disciplinas fundamentais temos muitas outras (obrigatórias ou não) que permitem ao aluno ter uma visão geral de diversas áreas de pesquisa em Ciência da Computação.

Em resumo, penso que a Iniciação Científica e o curso foram ambos muito interessantes e que a relação forte entre eles serviu para torná-los mais ricos em diversos sentidos.

Agradecimentos

Agradeço à minha família pelo apoio durante o curso, ao meu orientador Carlos Eduardo Ferreira pelo apoio e paciência durante estes anos e à Professora Yoshiko Wakabayashi, que aceitou supervisionar este trabalho. Há muitos outros que gostaria de agradecer, mas para minimizar o perigo de esquecer alguém, resolvi agradecer apenas aqueles mais diretamente envolvidos.

Finalmente, gostaria de agradecer meus amigos do BCC-2000. Certamente, estes quatro anos não seriam tão divertidos sem eles!

Bibliography

Dui94
C. W. Duin.
Steiner's Problem in Graphs.
Tese de doutorado, Universiteit van Amsterdam, 1994.

DV89
C. W. Duin e A. Volgenant.
Reduction tests for the Steiner problem in graphs.
Networks, 19:549-567, 1989.

Fer89
C. E. Ferreira.
O problema de Steiner em grafos: Uma abordagem poliédrica.
Dissertação de mestrado, Instituto de Matemática e Estatística da USP, 1989.

GKR00
N. Garg, G. Konjevod, e R. Ravi.
A polylogarithmic approximation algorithm for the group Steiner tree problem.
Journal of Algorithms, 37(1):66-84, 2000.

HRW92
F. K. Hwang, D. S. Richards, e P. Winter.
The Steiner Tree Problem, volume 53 de Annals of Discrete Mathematics.
North-Holland, 1992.

Kar72
R. M. Karp.
Reducibility among combinatorial problems.
In Miller e Thatcher, editores, Complexity of Computer Computations, p. 85-103. Plenum Press, New York, 1972.

RW90
G. Reich e P. Widmayer.
Beyond Steiner's problem: A VLSI oriented generalization.
In Graph-Theoretic Concepts in Computer Science WG89, volume 411 de Lecture Notes in Computer Science, p. 196-210. Springer, 1990.

RZ00
A. Rohe e M. Zachariasen.
Rectilinear group Steiner trees and applications in VLSI design.
Technical Report 00906, Institute for Discrete Mathemathics, 2000.

UAR99
E. Uchoa, M. P. Aragão, e C. Ribeiro.
Preprocessing Steiner problems from VLSI layout.
Technical Report MCC 32/99, Pontifícia Universidade Católica do Rio de Janeiro, 1999.

About this document ...

Estratégias para Solução de Problemas de Otimização Combinatória

This document was generated using the LaTeX2HTML translator Version 99.2beta6 (1.42)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -white -no_navigation -no_math form.tex

The translation was initiated by Fernando Mario de Oliveira Filho on 2003-12-06

Footnotes

... condutoras.1
Em problemas de roteamento é comum termos de ligar diversos conjuntos de componentes através de diferentes redes condutoras que devem ser disjuntas. Não trataremos deste caso aqui, suporemos que temos de conectar todos os componentes utilizando a mesma rede condutora.
... retilinear2
A distância retilinear entre os pontos $(x_1, y_1)$ e $(x_2, y_2)$ é $\modl{x_2 - x_1} + \modl{y_2 - y_1}$.

Fernando Mario de Oliveira Filho 2003-12-06